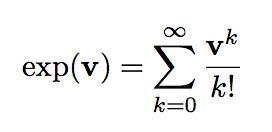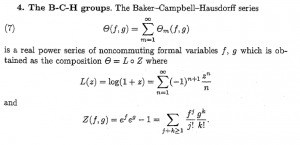Discussed topics
1) According to A. Kirillov reference, the formula
holds for any Lie group and Lie algebra subset of the same bigger algebra (as in the case of matrix lie group). Are we sure it hold also in the case of diffeomorphisms? I know this is an old topic (see below), but if we assume, as working hypothesis, that it is true, then it may open some possibilities for the next point.
2) Accelerating convergence series: using methodologies from a theory developed around ’80 and still evolving now, we can use these formulas
to compute the bch and, so accelerate it as series.
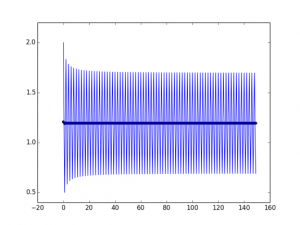
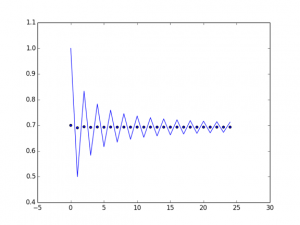
The next two examples represents log(n) and 1/n*(n+1) for n positive integer in the continuous blue line. The dots plot represents the Aitken accelerating method (one of the older and less sophisticated).
(this second serie in particular is super slow to converge to 5/4, but the accelerating one gets on this value after a couple of steps).
It seems promising, even if, for our case it may lead to some difficulties in implementing the svf in a suitable form to applies these methods.
4) Fast update about the state of the MRes. Now it is on gitlab, I will keep on working daily. Any suggestion about math, methods, typo for its improvement are welcome!! About the style and outline, in order to avoid any future possible clashes between parts I will bother only Tom to have draft’s review and suggestions (unfortunately for him).
—————–
About the computation of the exp.
There is something puzzling us:
Let
f(u) = ∑ u^k / k!
we then have
f(tu) = ∑ (tu)^k / k!
Let’s look at the first two terms here:
f(tu) = Id + tu + .5 * ( tu ○ tu ) + …
Note that I intentionally haven’t replaced the dots by O(t²)
Now let’s apply and expand this at a given point x for a small t
f(tu)(x) = x + tu(x) + .5 * ( tu ○ tu )(x) + …
= x + tu(x) + .5 * t[ u( tu(x) ) ] + …
= x + tu(x) + .5 * t[ u(0) + t ∇u(0).u(x) + … ) + …
= x + t * [ u(x) + .5 u(0) ] + 0.5 t² ∇u(0).u(x) + …
So it looks like f does not behave as we would like it to. Indeed, it appears as if
lim_{t→0} ( f(tu) -f(0) ) / t = u(x) + ( ∑_{k>1} 1 / k! ) u(0)
At the core of the previous equations is there the following interpretation of the composition:
u( tu(x)) = u(0) + t∇u(0).u(x) + …
When we have g , G subset of some bigger algebra A,
the product in the algebra A (usually is not commutative), coincides with the composition and is is compatible with the scalar product – take matrices, quaternions, or even infinite case as polynomials -.
http://en.wikipedia.org/wiki/Algebra_over_a_field#Definition
If we are sure that lie group of diffeomorphisms and lie algebra are subset of the same A, then (tu ○ tu)(x) = t^2 u(u(x)) – as a consequence of the compatibility of the scalar product.
But what is this product of diffeomorphisms in this bigger algebra A?
If diff(omega) and vect(omega) are subsets of a bigger algebra A, then we have an object A that contains vectors and transformations and an operation of multiplication compatible between them and between the scalar product.
How would we compute this u(u(x)) for u vectors in g and in A?
—
I think that diff(omega) and vect(omega) are not subset of the same bigger algebra A in the usual sense. But the commonalities that you see are there and there is still some structure that contains them both:
I thought a lot about it and I think it is a bigger algebra A that contains g in a proper sense, that it is defined as a quotient, and contains also G, not in a proper sense, but as the limit of the degree of the quotient that defines A. Namely
\oplus is the log-composition and Ad are the lie bracket. If n=0 degree of the polynomial, in this algebra all the lie bracket vanishes, it is still a lie algebra but we have no way to reach the group from there. If n = inf then we have infinite lie bracket in this object and we can reach G as log composition, directly with the BCH.
In this settings operations are compatible, and the log-composition is the operation that make A as a structure that contains -in some sense as a limit- G as group, and that is compatible with the Lie algebra.
—–