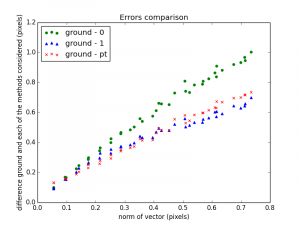
Still half disappointing results from the code. Here we have some graph to compare parallel transport method with the bch 0 and bch 1.
There is a range in which parallel transport seems to doing better.
Future work is oriented toward the investigation of new numerical computation of the exponential using Trapezoidal method and Runge Kutta.
To compare the results a norm defined over the element of the group is improperly considered: this take into account the nature of the deformations, that, as vector fields defined over a grid (5d images) can be considered as an embedding in the space of matrices, where several norms are at our disposal.
Why we prefer to consider the norm in the tangent space instead of the norm on the embedding space of the group of transformations?
$$
\mahtbb{G} \subseteq \{ f:\Omega \rightarrow \Omega \mid f \text{ vector field }\}
$$
A metric can be defined only on a vector space, where sum and scalar product are defined. In the case of diffeomorphisms we do not have any, and the sum and scalar product we can consider hinerited from the structure of the module defined by vector fields are not closed under these operations. Sum of two diffeomorphisms is not a diffeomorphisms, even if it can be expressed as a vector space.
A second hint is about the analogies that could be explored between the taylor expansion of the bch and the derivative of the exponential map:
http://en.wikipedia.org/wiki/Derivative_of_the_exponential_map
Further discussions with Marco led to consider the Lie derivative as one of the elementary tools in differential geometry.