Discussed topics:
Point of the situation of the implementation of exp function.
Update about the MRes situation
Discussion about the nature of the group of diffeomorphisms and its Lie algebra as subset of the same bigger algebra, defined by the operators.
—-
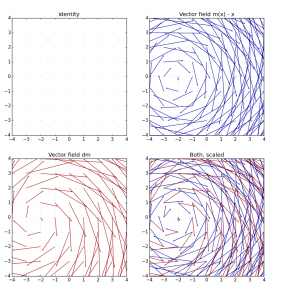
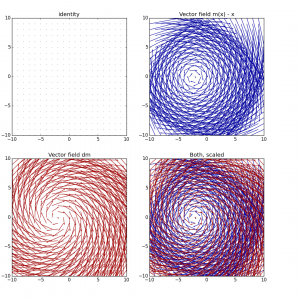
Results of the numerical tests for the computation of the BCH formula applied to discretized tangent vector to the space of diffeomorphisms Lie(Diff(R^n)).
The BCH shows converging behaviour appears to be confirmed for this infinite dimensional Lie group of diffeomorphisms on R^3.
The curious fact is that the proof of Dynkin for the BCH formula relies on the possibility of expanding the exponential and the logarithm in Taylor series: and they hold only when the Lie group and the Lie algebra are subset of a bigger algebra.
So there are two possibilities:
1) The BCH can be proved without using these expansions.
2) These expansions holds for the group of diffeomorphisms of R^3.
It would mean that Diff(R^n) and Lie(Diff(R^n)) are a subset of a bigger algebra (the algebra of the continuous operators from Omega to Omega where the product is the composition) so that the sum of tangent vector to the manifold Diff (every smooth vector field in R^n) is defined in the group of diffeomorphisms (every smooth invertible function in R^n) an the composition is compatible with the product – exactly as in the case of the matrix Lie group.
The sub algebra of diffeomorphisms has as its Lie group the differentiable invertible operator. Starting from the Diffeomorphisms over Omega, their tangent vectors are vector field whose composition is the their usual composition as function (vector fields are functions after all).
This may work thanks to the fact that we consider only the set of diffeomorphism that are the identity outside Omega: this make the group of diffeomorphisms a group that does not need to rely on any Frechet space and it is well behaved, exactly as the matrix Lie groups. These reference
http://arxiv.org/pdf/1211.5704v2.pdf subsection 3
http://www.mat.univie.ac.at/~michor/mf-smo-2.pdf
seems to confirm.
In this case the approximation exp(v) \simeq id + v is the first order of the taylor series, as well as, if we start from the vector field v, an approximation of the tangent vector as the actual vector field obtained by the transformation T := exp(v) – id \simeq v.
In the following picture SE2 transformations
Parameters of the transformation are theta = – pi / 3, tx, ty = -1, -2
having the same behaviour of the translation of the action of an element of SO2, since
exp(v)(p) = R.p + T = R.(p+R^{-1).T) = R.p’
—- Meeting with Marco
On Thursday a second meeting with Marco (just before his fly to Washington) about the MRes.
Suggestions about introduction and corrections of -many- mistakes and typo have been proposed.
To have a more organic work he suggested to collect every part about the parametrisation of SVF in a single section instead of having them scattered in more than one part.
He suggested in addition to smooth various parts of the research, in order to reduce the “copy and paste” effect on the reader and to have a more coherent and readable work. We came out with the idea of implementing a Gaussian smoother for essays and dissertations to make these kind of works automatic.
— Suggestions from Marc
Due to the difficulties in defining reliable ranodm SVF, we decided to move toward the utilisation of Real dataset and SVF from real cases: MIRADA dataset and Nifty reg may provide the required SVF with the following command:
reg_aladin -ref ../AD_0_baseline.nii -flo ../CTL_0_baseline.nii -aff matrix.txt -res affine_refAD0_floCTL0.nii.gz -lp 1 -speeeeed
reg_f3d -ref ../AD_0_baseline.nii -flo affine_refAD0_floCTL0.nii.gz -cpp cpp_refAD0_floCTL0.nii.gz -res res_refAD0_floCTL0.nii.gz -vel -lp 1 -maxit 10
reg_transform -ref ../AD_0_baseline.nii -flow cpp_refAD0_floCTL0.nii.gz flow_refAD0_floCTL0.nii.gz
—– BIBLIOGRAPHY:
scaling and squaring is called “Phase Flow method”:
Ying, L., & Candès, E. J. (2006). The phase flow method. Journal of Computational Physics, 220(1), 184–215. doi:10.1016/j.jcp.2006.05.008
Teitzel, C., Grosso, R., & Ertl, T. (1997). Efficient and Reliable Integration Methods for Particle Tracing in Unsteady Flows on Discrete Meshes. In Visualization in Scientific Computing ’97 (pp. 31–41). doi:10.1007/978-3-7091-6876-9_4
Wiki exponential integrator methods
https://en.wikipedia.org/wiki/Numerical_methods_for_ordinary_differential_equations#First-order_exponential_integrator_method
—– Mechanics
Holm, Darryl D., et al. Geometric mechanics and symmetry: from finite to infinite dimensions. London: Oxford University Press, 2009.
—– (Discrete) difference equation
http://www.cambridge.org/gb/academic/subjects/mathematics/differential-and-integral-equations-dynamical-systems-and-co/difference-equations-differential-equation-methods